데이터 전처리 : 순차적 특성 선택
March 20, 2022, 8:27 p.m.
모델을 훈련하다 보면 훈련셋에서의 성능이 테스트셋에서의 성능보다 많이 높게 나오는 경우가 있습니다. 즉, 일반화 성능이 안좋은 것인데요. 모델이 훈련셋에 과대적합 되었기 때문에 이러한 일이 발생하게 됩니다.
과대적합을 막기 위해서는 모델을 최대한 간단하게 만드는 것이 중요합니다. 필요없는 특성까지 반영하여 모델을 훈련시키게 되면 데이터의 의미를 찾지 못하기 때문에 일반화하지 못하고 훈련 데이터에만 과대적합하게 되는 것이죠.
이번 포스트에서는 의미 있는 특성을 탐욕적으로 찾는(Greedy Search) 방법인 순차적 특성 선택 알고리즘에 대해서 알아보도록 하겠습니다.
1. 순차적 특성 선택 알고리즘이란?
순차적 특성 선택이란 훈련 데이터의 특성들 중에서 제일 의미 없는 특성부터 한개씩 줄여 나가면서 성능이 좋은 가장 간단한 모델을 찾는 알고리즘입니다. 각 특성관의 관계에 대해서 하나도 몰라도 됩니다. 제거했을때 성능이 가장 좋은 경우를 쫓아 가는 것입니다.
먼저 임의로 특성을 1개 없애보고 훈련시킨후 모델의 성능을 평가합니다.
이것을 모든 특성에 대해서 진행하고 그 중에서 제거 했을 때 평가 성능이 제일 좋았던 특성을 제거합니다.
이 과정을 반복하여 특성의 개수가 정해진 개수까지 줄여지면 종료합니다. 간단하죠?
파이썬으로 한번 구현해 보겠습니다.
2. 파이썬 구현
python machine learning 2nd ed. 책을 참고 하였습니다.
from itertools import combinations //특성간의 조합을 쉽게 얻어낼 수 있는 Combinations(조합)
from sklearn.metrics import accuracy_score // 모델의 성능을 평가할 accuracy score
from sklearn.model_selection import train_test_split //훈련할 데이터와 테스트할 데이터를 나누어줌
class Sequential_Selection():
def __init__(self, estimator, k_features, scoring=accuracy_score, test_size=0.25, random_state=1):
self.scoring = scoring
self.estimator = estimator
self.k_features = k_features
self.test_size = test_size
self.random_state = random_state
def fit(self, X, y):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=self.test_size, random_state=self.random_state)
//훈련 셋과 테스트 셋으로 나누어줌.
dim = X_train.shape[1] // 특성의 차원
self.indices_ = tuple(range(dim)) // 사용할 특성 튜플
self.subsets_ = [self.indices_] // 튜플을 담을 최종 리스트
score = self._calc_score(X_train, y_train, X_test, y_test, self.indices_) // 모델 평가(현재는 모든 특성 사용)
self.scores_ = [score] //정확도 점수 추가
while dim > self.k_features: //정해진 특성 개수에 도달할때까지
scores = []
subsets = []
for p in combinations(self.indices_, r=dim -1): // 특성에서 1개를 뺀 조합을 내놓는 이터레이터
score = self._calc_score(X_train, y_train, X_test, y_test, p) // 해당 조합으로 모델 평가
scores.append(score) //점수 추가
subsets.append(p) //해당 조합 추가
best = np.argmax(scores) //추가된 점수중에서 가장 큰 점수의 인덱스를 구함
self.indices_ = subsets[best] // 해당 인덱스로 해당 조합을 불러옴
self.subsets_.append(self.indices_) // 해당 조합을 최종 리스트에 추가
dim = dim -1 //특성 1개 줄임!
self.scores_.append(scores[best])
self.k_score_ = self.scores_[-1] //최종 점수
return self
def transform(self, X): // fit()을 통해 특성제거된 데이터 리턴
return X.iloc[:, list(self.indices_)]
def _calc_score(self, X_train, y_train, X_test, y_test, indices): // 데이터와 특성 정보를 받아 모델 훈련후 점수 리턴
self.estimator.fit(X_train.iloc[:, list(indices)], y_train)
y_pred = self.estimator.predict(X_test.iloc[:,list(indices)])
score = self.scoring(y_test, y_pred)
return score
3. 적용하기
해당 알고리즘을 직접 적용해 보고, 특성 조합에 따른 모델의 성능을 그래프로 그려볼게요.
import numpy as np
import pandas as pd
data = pd.read_csv('/content/drive/MyDrive/Kaggle/hand_gesture_data/train.csv')
id sensor_1 sensor_2 sensor_3 sensor_4 sensor_5 sensor_6 \
0 1 -6.149463 -0.929714 9.058368 -7.017854 -2.958471 0.179233
1 2 -2.238836 -1.003511 5.098079 -10.880357 -0.804562 -2.992123
2 3 19.087934 -2.092514 0.946750 -21.831788 9.119235 17.853587
3 4 -2.211629 -1.930904 21.888406 -3.067560 -0.240634 2.985056
4 5 3.953852 2.964892 -36.044802 0.899838 26.930210 11.004409
... ... ... ... ... ... ... ...
2330 2331 -3.971043 39.913391 16.034626 -19.067697 8.061361 -70.916786
2331 2332 -3.011710 -4.060355 -1.046067 4.178137 -2.003243 -2.895017
2332 2333 -9.001824 5.985711 -8.146347 -10.902201 5.102105 8.133692
2333 2334 -3.987992 3.011460 -11.949323 -3.810885 16.880234 -5.150117
2334 2335 -1.838225 -7.023497 -45.877365 20.026927 4.058551 8.062100
sensor_7 sensor_8 sensor_9 ... sensor_24 sensor_25 sensor_26 \
0 -0.956591 -0.972401 5.956213 ... -7.026436 -6.006282 -6.005836
1 26.972724 -8.900861 -5.968298 ... -1.996714 -7.933806 -3.136773
2 -21.069954 -15.933212 -9.016039 ... -6.889685 54.052330 -6.109238
3 -29.073369 0.200774 -1.043742 ... -2.126170 -1.035526 2.178769
4 -21.962423 -11.950189 -20.933785 ... -2.051761 10.917567 1.905335
... ... ... ... ... ... ... ...
2330 -39.937026 12.834223 -21.937973 ... 3.086417 -4.954858 -11.106802
2331 -2.766757 -29.099123 -4.208953 ... 6.871938 -0.134367 -0.867018
2332 32.877614 -3.017438 -3.174442 ... -7.952857 2.049467 -5.825790
2333 9.182801 4.960190 -21.002525 ... 3.080276 2.054739 -1.052350
2334 19.083782 -21.881795 -9.106341 ... 31.130021 5.121935 -1.003704
sensor_27 sensor_28 sensor_29 sensor_30 sensor_31 sensor_32 target
0 7.043084 21.884650 -3.064152 -5.247552 -6.026107 -11.990822 1
1 8.774211 10.944759 9.858186 -0.969241 -3.935553 -15.892421 1
2 12.154595 6.095989 -40.195088 -3.958124 -8.079537 -5.160090 0
3 10.032723 -1.010897 -3.912848 -2.980338 -12.983597 -3.001077 1
4 -13.004707 17.169552 2.105194 3.967986 11.861657 -27.088846 2
... ... ... ... ... ... ... ...
2330 -37.863399 31.069292 -4.097017 -13.095192 -5.150284 8.016265 3
2331 23.892336 -11.977934 1.984203 0.891666 28.822082 -0.878670 3
2332 -37.989569 15.014132 1.160272 -11.135889 -7.035763 -0.930067 3
2333 -6.019488 -7.075333 -5.826058 -3.989168 14.916905 -12.093426 1
2334 -58.953961 -22.095226 -0.898581 1.164833 -21.977991 -13.060285 2
데이터를 가져왔습니다. 센서 데이터와 target 레이블로 이루어져 있는 데이터네요.
y = data.iloc[:, -1]
X = data.iloc[:,1:-1]
레이블값과 데이터를 나눕니다.
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver='liblinear', multi_class='auto',C=100.0, random_state=78)
간단한 로지스틱 회귀 분류 모델을 가져왔습니다.
불러온 데이터와 모델로 순차적 특성 선택을 적용해 보겠습니다.
ss = Sequential_Selection(lr, 6)
ss.fit(X, y)
특성을 6개로 줄이는 것을 목표로 훈련이 완료되었습니다.
그럼 Sequential_Selection 클래스에 있는 scores_ 리스트를 그래프로 그려볼까요?
x축은 특성의 개수입니다.
import matplotlib.pyplot as plt
plt.plot([len(k) for k in ss.subsets_], ss.scores_, marker='o')
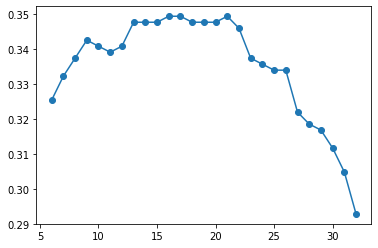
와우! 특성 선택의 효과가 있는 것 같네요.
특성이 32개일때는 정확도가 낮다가 특성의 개수가 17~21사이에서 제일 좋은 성능을 보이고, 그다음엔 다시 정확도가 내려가는 모습을 볼 수 있습니다.
transform() 메서드를 적용하면 특성을 6개로 줄인 것이 적용됩니다.
x_trans = ss.transform(X)
sensor_3 sensor_5 sensor_6 sensor_12 sensor_15 sensor_18
0 9.058368 -2.958471 0.179233 -4.061254 -13.956994 -1.957662
1 5.098079 -0.804562 -2.992123 -5.046353 -25.072542 -3.998035
2 0.946750 9.119235 17.853587 -9.000630 -10.954367 -6.118940
3 21.888406 -0.240634 2.985056 -0.069867 5.127194 -1.099702
4 -36.044802 26.930210 11.004409 5.961219 -9.970728 -3.161698
... ... ... ... ... ... ...
2330 16.034626 8.061361 -70.916786 11.739764 62.908697 -5.847474
2331 -1.046067 -2.003243 -2.895017 28.906574 -1.957465 -1.883162
2332 -8.146347 5.102105 8.133692 3.966698 -40.966145 -5.022308
2333 -11.949323 16.880234 -5.150117 -4.015727 65.066757 8.861321
2334 -45.877365 4.058551 8.062100 -9.064997 -62.952969 -9.053823
가장 중요한 특성 6개만 남은 모습을 볼 수 있습니다.
그렇지만 아까 그래프를 봤듯이 특성의 개수가 17~21사이일때 가장 좋은 성능을 냈었죠? subsets_ 리스트에서 직접 해당 특성 리스트를 불러와 적용할 수도 있습니다.
x_trans_best = X.iloc[:, list(ss.subsets_[32-17])] // 특성을 17개로 줄였을 때
sensor_3 sensor_5 sensor_6 sensor_9 sensor_10 sensor_12 \
0 9.058368 -2.958471 0.179233 5.956213 4.145636 -4.061254
1 5.098079 -0.804562 -2.992123 -5.968298 -4.060134 -5.046353
2 0.946750 9.119235 17.853587 -9.016039 -5.975194 -9.000630
3 21.888406 -0.240634 2.985056 -1.043742 2.099845 -0.069867
4 -36.044802 26.930210 11.004409 -20.933785 -4.000506 5.961219
... ... ... ... ... ... ...
2330 16.034626 8.061361 -70.916786 -21.937973 14.942994 11.739764
2331 -1.046067 -2.003243 -2.895017 -4.208953 -4.793855 28.906574
2332 -8.146347 5.102105 8.133692 -3.174442 -5.724941 3.966698
2333 -11.949323 16.880234 -5.150117 -21.002525 -1.881519 -4.015727
2334 -45.877365 4.058551 8.062100 -9.106341 -1.056355 -9.064997
sensor_13 sensor_14 sensor_15 sensor_17 sensor_18 sensor_19 \
0 0.996632 -3.837345 -13.956994 2.130210 -1.957662 -1.149930
1 1.083819 3.978378 -25.072542 2.912269 -3.998035 6.069698
2 9.115957 12.097318 -10.954367 -19.069594 -6.118940 -5.001346
3 -0.114247 -1.896109 5.127194 2.970044 -1.099702 3.116767
4 9.907115 -0.067754 -9.970728 1.892233 -3.161698 -9.225990
... ... ... ... ... ... ...
2330 12.078842 7.000148 62.908697 -2.804120 -5.847474 -78.034200
2331 -1.865353 5.974470 -1.957465 -2.107972 -1.883162 -4.918032
2332 1.066745 3.988601 -40.966145 -5.877931 -5.022308 -25.948680
2333 -6.948209 -6.052921 65.066757 6.877978 8.861321 -15.161502
2334 10.027128 -2.950048 -62.952969 -26.725765 -9.053823 51.213548
sensor_20 sensor_21 sensor_22 sensor_25 sensor_26
0 6.082028 0.878612 5.093102 -6.006282 -6.005836
1 4.966187 1.994051 -1.132059 -7.933806 -3.136773
2 -9.105371 -9.894885 10.107614 54.052330 -6.109238
3 8.124209 -0.917418 -1.027199 -1.035526 2.178769
4 3.953956 -17.959652 -3.115491 10.917567 1.905335
... ... ... ... ... ...
2330 -6.052717 -8.027884 27.992994 -4.954858 -11.106802
2331 0.032044 -1.043068 -3.980494 -0.134367 -0.867018
2332 -15.880140 3.976966 10.996415 2.049467 -5.825790
2333 2.050648 -0.060606 -1.081436 2.054739 -1.052350
2334 -10.993737 7.971206 7.820410 5.121935 -1.003704
[2335 rows x 17 columns]
특성이 17개로 줄여진 모습입니다.
특성 선택을 통해서 차원을 줄이고 일반화 성능을 높이는 방법을 알아보았는데요, 가장 무식하게 접근하는 방법이기도 하지만 가장 간단한 방법이기도 합니다. 데이터에 따라서 순차적 특성 선택으로 특성을 줄여 모델의 차원을 낮추고 일반화 성능을 올려보세요.