머신러닝 데이터 선형 판별 분석 : LDA
April 3, 2022, 11:26 p.m.
선형 판별 분석, LDA는 규제가 없는 분류 모델에서 고차원의 데이터에 의한 과대 적합을 줄이고 특성을 추출하기 위한 기법중에 하나입니다.
이전에 주성분 분석(PCA)에 대해 알아보았는데 기본적으로 LDA도 PCA와 비슷합니다.
PCA는 분산이 최대로 되는 성분을 축으로 삼는 반면에 LDA는 클래스를 최적으로 구분할 수 있는 성분을 축으로 삼습니다. 그렇기 때문에 분류 문제에서 PCA보다 좋은 성능을 기대할 수 있습니다.
LDA는 데이터가 정규분포라고 가정합니다. 그렇기 때문에 데이터에 LDA를 적용하기 전에 표준화 전처리를 해주는 것이 유리합니다.
그럼 사이킷런을 통해서 LDA를 데이터에 적용해 보도록 하겠습니다.
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y, random_state=0)
분류 문제에서 가장 유명한 와인 분류 데이터를 불러온 후 훈련 셋과 테스트 셋으로 나누어 주었습니다.
X_train.shape
(124, 13)
13개의 특성을 가진 데이터라는 것을 볼 수 있네요.
이제 LDA를 통해 특성을 추출하여 특성의 차원을 낮추어 보겠습니다.
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc_train = sc.fit_transform(X_train)
먼저 표준화 전처리를 해주었습니다. LDA를 적용하고 shape를 통해 적용이 완료되었는지 보겠습니다.
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
lda_X = lda.fit_transform(X_train, y_train)
lda_X.shape
(124, 2)
특성이 2개로 줄어든 모습을 볼 수 있네요! 과연 이 특성 축이 레이블을 최대로 나눌 수 있는 축인지 산점도로 확인해 보겠습니다.
from matplotlib import pyplot as plt
plt.scatter(lda_X[y_train==1,0], lda_X[y_train==1,1])
plt.scatter(lda_X[y_train==2,0], lda_X[y_train==2,1])
plt.scatter(lda_X[y_train==3,0], lda_X[y_train==3,1])
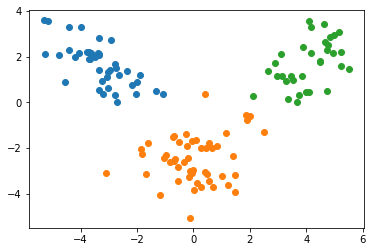
산점도를 보면 직선으로 세가지 레이블을 잘 나눌 수 있을 것 같습니다! LDA가 특성을 잘 추출했다는 뜻이고, 로지스틱 회귀 같은 선형 모델을 사용한다면 완벽하게 분류해낼 수 있을 것입니다.
이번 포스트에서는 선형 판별 분석, LDA에 대해서 알아보았습니다. 클래스 레이블이 있는 분류 문제에서 LDA는 선형으로 클래스 레이블을 분류 할 수 있도록 특성을 추출해 줍니다. 분류 문제에서 PCA보다 유용하게 쓸 수 있으니 사용해 보시기 바랍니다.
사이킷런 scikit-learn LDA